TechEdgeUp - Vernetzung begreifen

Was zeichnet Digitalisierung eigentlich aus?

Obgleich der Begriff „Digitalisierung“ inzwischen täglich allgegenwärtig ist, fällt eine Konkretisierung des Begriffs eher schwer. Die Frage, was Digitalisierung sei, bleibt allzu oft mit trivialen Antworten wie „Laptop & WLAN“ oder auch mit „Smartboards & Tablets“ hinsichtlich dem Wesen von Digitalisierung bestenfalls angerissen.

Die Bedeutung, die dem Thema „Vernetzung“ zur Beantwortung der obigen Fragen zukommt, wird dabei teilweise ausgeblendet oder in den Hintergrund gerückt. Doch das, was heutzutage als Digitalisierung bezeichnet wird, ist primär durch Vernetzung gekennzeichnet.

Zum Verständnis des Sachverhalts sollten zunächts Aspekte zur Digitalisierung beleuchtet werden:

• Digitalisierung als Technik
• Eigenschaften von Digitalisaten
• Digitalisierung als gesellschaftlicher Wandel

Der Begriff „digital“ leitet sich vom lateinischen digitus „Finger“ ab. Es meint etwas mit den Fingern abzählbares.

Um Digitalisierung im technischen Sinne zu verstehen, muss zunächst der Begriff „Diskretisierung“ erklärt werden. Nachfolgend können dann diskretisierte Wert digital dargestellt werden, was dann als Digitalisierung bezeichnet wird.

Unter Diskretisierung versteht man die mathematisch diskrete Faltung eines analogen, zeitkontinuierlichen Signals mit einer Kamm-Funktion. Im folgenden Bild ist das analoge, grüne Signal ein Ausschnitt einer sinussoidalen Funktion. Die blaue Funktion ist die Kamm-Funktion. Aus der Faltung ergibt sich die braune Funktion.

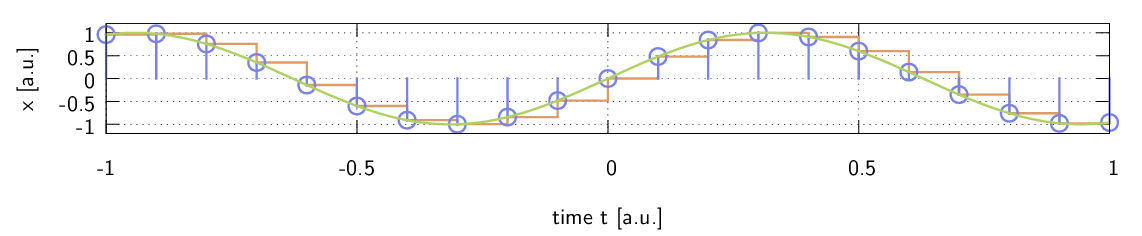
Streng genommen ist das Ergebnis, die braune Funktion, immer noch zeitkontinuierlich. Da aber das Signal von einem Peak zum nächsten Peak der blauen Kamm-Funktion beim diskreten, braunen Signal konstant beleibt, kann eine Zuordnung des Werts zum ersten Peak erfolgen, also „diskret“ zum Zeitpunkt des Peaks. Jeder Peak der blauen Funktion verweist auf einen Sample, dessen Wert aus der braunen Funktion zugeordnet werden kann. Im Ergebnis ergibt sich also eine Folge aus Samples. Die Samplerate, aus dem Audio-Bereich bekannt, sagt aus, wie viele dieser Samples in einer Sekunde genutzt werden, also wie viele Samples pro Sekunde verwendet werden.

Erkennbar kann die braune diskrete Funktion nicht mehr alle Werte annehmen, wie die grüne, analoge Funktion. Die Auflösung der diskreten Werte ist schlechter, als die Originalfunktion. In unserer Abbildung sind 6 Stufen erkennbar, also gibt es nur sechs verschiedene Werte, sodass die sechs Zahlen mit der Null, also von 0-5, zur eindeutigen Bezeichnung des realen Werts ausreichen würden. Diese sechs Zahlen sind mit Fingern einzeln abzählbar, was als digital bezeichnet wird. Statt dem gesuchten Wert, genügt zu schauen, ob der Finger n gezeigt wird oder nicht. Ein Finger kann also die Werte ja/nein bzw. 0/1 bzw. da/nicht-da annehmen - als binär bezeichnet, was zweizählig bedeutet. Das lateinische bina meint doppelt oder paarweise. Jeder Finger also ein Bit. Die Folge der Samples kann also aus Bits dargestellt werden.

Wenn nun die Abtastfunktion hinsichtlich Auslenkung x und der Zeit t sehr feingliedrig ausgestaltet wird, so ist auch das Ergebnis der Digitalisierung sehr feingliedrig. Liegt dieses Verfahren weit über der menschlichen Auflösung, kann das Ergebnis vom analogen Signal nicht mehr unterschieden werden, wie beispielsweise bei digitaler Musik. Für Musikdateien bezeichnet die Samplerate wie schnell abgetastet wird. Ein weitere Größe, die Speichertiefe, gibt Auskunft, wie viel Werte für die Auslenkung x veranschlagt werden. Ein WAV-Datei hat typisch eine Abtastrate von \(44100\,\mathrm{Hz}\) mit \(16\,\mathrm{Bit}\) Speichertiefe pro Kanal, was sich also bei Stereo eine Datenrate zu \(2 \cdot 16\,\mathrm{Bit} \cdot 44100\,\mathrm{Hz} = 1411200\,\mathrm{Bit/s} \approx 1,5\,\mathrm{MBit/s}\) ergibt.

Das gilt einerseits für die Zeit t zur obigen sinussoidalen Funktion, was bei Musik in die Samplerate übergeht, also wie schnell wird abgetastet, und anderseits für die Auslenkung x mit der Samplerate in der Datenrate aufgeht. Um zu verstehen, warum nun die digitale Musik so glasklar und störungsarm ist, muss man sich den Eigenschaften von Digitalisaten klären.

Ein Digitalisat ist ein Datenverbund, dessen Daten digital, also fingerhaft abzählbar, vorliegen.

Sobald entscheiden werden kann, ob ein Finger gesetzt ist oder nicht, kann zwischen 0 oder 1 unterscheiden werden. Die Signalqualität, also ob ein Finger vollständig gestreckt ist, spielt nur dann eine Rolle, wenn die Fingerstreckung die Entscheidungsschwelle noch erreicht. Bereits hier verhalten sich digitale Signale anders als analoge Signale. Die nachfolgenden Eigenschaften von Digitalisaten sind allesamt komplementär zu analogen Entsprechungen.

• Die Kopie eines Digitalisats ist vom Original hinsichtlich des Informationsgehalts nicht zu unterscheiden.
• Jedes Digitalisat kann (bitweise) kopiert werden.
• Die Kopierkosten eines Digitalisats gehen gegen null.
• Die Speicherkosten eines Digitalisats gehen gegen null.
• Die Transportkosten gehen gegen null.
• Die potentiell mögliche Speicherdauer eines digitalen Speichermediums ist hoch. (Keilschrift, ca. 5000 Jahre)

Ein digitales Musikstück kann schnell und beliebig oft kopiert, immer günstig versendet und stets preiswert in großen Mengen abgespeichert werden, wobei der Informationsgehalt, und somit auch die Qualität, der Kopie zum Original ununterscheidbar bleibt. Genau entgegengesetzt verhält sich dieser Zusammenhang bei einer analogen Schallplatte; mit jeder Kopie der Kopie werden auch kleine Störungen mit vervielfältigt und hinzukommende Störungen lassen die Qualität merklich sinken.

Wenn digitale Geräte vernetzt Daten austauschen, werden alle obigen Eigenschaften von Digitalisaten genutzt. Jeder Zugriff auf eine Datei oder Web-Seite erzeugt eine qualitativ äquivalente Kopie des Originals. Jeder Teilnehmer eines digitalen Datentauschs hat dieselbe Kopie wie das Original, wobei Kopie und Original vom Informationsgehalt ununterscheidbar sind. Mit weiteren zusätzlichen Prüfverfahren kann auch die Übertragung sichergestellt werden: Da digitale Signale abzählbare Signale sind, kann durch einfaches mitzählen geprüft werden, ob alle Bits, also alle Daten, beim Empfänger gelandet sind. Erst durch Vernetzung erhalten Laptops, Smartboard oder Tablets einen Mehrwert, der über den des einzelnen Geräts hinausgeht.

Der gesellschaftliche Begriff „Digitalisierung“ ist also bei vernetzten Kommunikationspartner das Nutzen der Eigenschaften von Digitalisaten. Daher fällt dem Thema „Vernetzung“ eine besondere Rolle zu, deshalb muss man, um Digitalisierung zu verstehen, „Vernetzung begreifen“.